- Additives
- Instruments

In addition to the subjective perception of viscosity, the flow behavior of substances can also be determined by measurement using suitable devices (viscometers, rheometers). In order to be able to describe different flow behavior, important rheological terms are first defined. The necessary relationships can be explained using the so-called Newtonian two-plate model. Geometrically and physically measured variables are brought into relationship for this purpose and can be represented as follows:
A fluid is placed between two plates of area A. The plates are spaced by a distance of d. The fluid is divided mentally into thin layers (lamellae), which run parallel to the two plates. If the upper plate is moved by the force F parallel to the lower one with the velocity v, the fluid near the upper plate moves with a much higher velocity than the one near the lower plate. A (linear) velocity gradient is established between the fluid lamellae. In order to quantify these relationships, several variables are considered and placed in relation to each other. Finally, the definition of viscosity results from this consideration.
The calculation of viscosity is derived from the Newtonian two-plate model. It is calculated from the quotient of the shear stress () and the shear rate (
).
The shear stress is the force F per area A needed to move a material. For materials with different flowing resistance, different forces are required to move the material at the same speed. The smaller the area, the lower the force required to move the material at the same rate, and vice versa. (Example: painting with wide versus narrow brush).
= F/A
The shear rate (formerly D) is the ratio of the velocity v to the distance d. If a material is applied (coated) at the same velocity but with different film thicknesses, this results in different shear rates. The lower the coating thickness, the higher the shear rate and vice versa.
= v/d
Viscosity is defined as the quotient of shear stress and shear rate
. It is the measure of resistance to flow. ƞ =
/

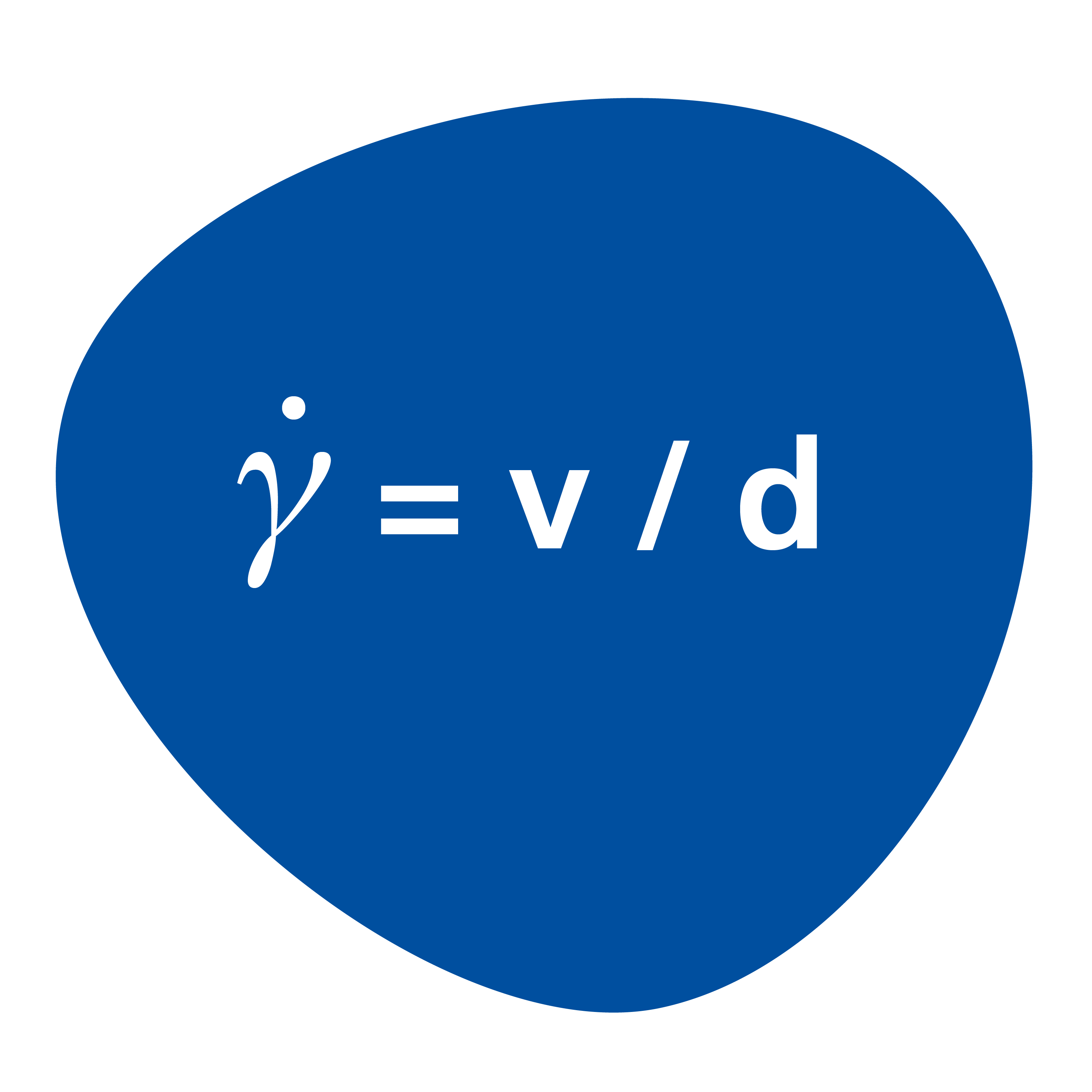
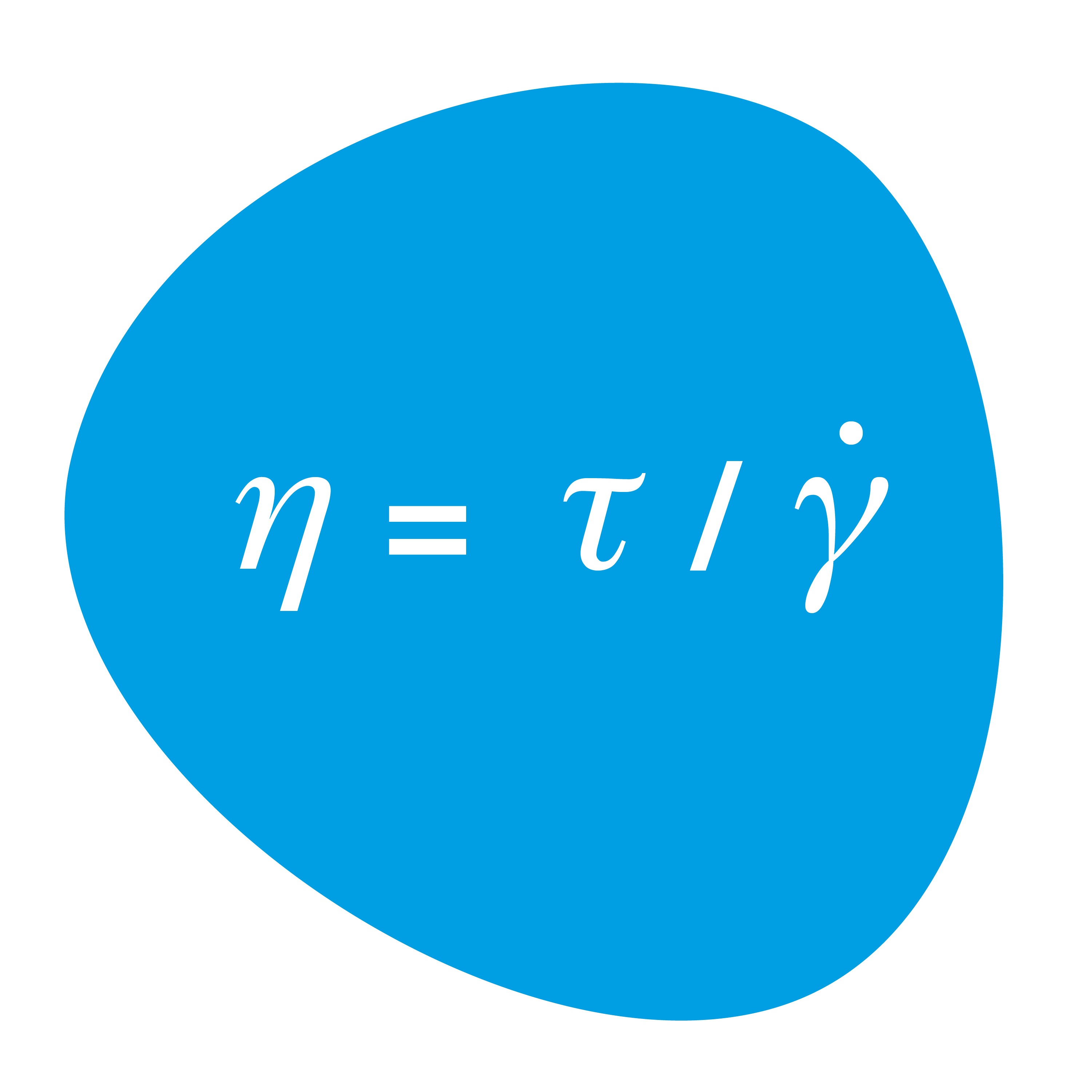
A Newtonian fluid is characterized by the fact that its viscosity is always the same, regardless of the stress applied. Its viscosity is a material constant (see two-plate model).
The advantage of Newtonian fluids, depending on the viscosity, is good flow in combination with good substrate wetting. Disadvantages are the tendency to sag on vertical surfaces and reduced storage stability (settling) of formulations with solid components (pigments, fillers).
Rheology additives can be used to avoid the disadvantages of Newtonian fluids. These lead to altered flow behavior, such as pseudoplastic or thixotropic.
In practice, a Newtonian flow behavior is often not desired due to the disadvantages explained. Instead, a structural viscous behavior can compensate the disadvantages.
Characteristic of a structural viscous - also called pseudoplastic - flow behavior is a high viscosity at rest (storage), which decreases with increasing shear stress (shear thinning) and immediately builds up again with decreasing shear stress.
Thixotropic flow behavior is also shear-thinning. However, after shear stress is removed, the viscosity builds up again with time delay.
The level of additive dosage and the solids content of a formulation have an influence on the speed of structure formation (the higher, the faster).
A special feature for shear-thinning substances can be the formation of a yield point. In this case, the internal structure of the substance is so strong that the substance is deformed before flow can occur, despite the applied force. Only if the applied force is strong enough that the internal structure is destroyed does the flow begin.
The flow behaviors described so far occur most frequently in practice and are characterized by shear-thinning flow behavior. By contrast, so-called dilatant flow behavior, in which viscosity increases with increasing shear (shear-thickening), occurs far more rarely. Examples of this are highly filled suspensions or higher molecular weight liquid polymers.
To characterize the rheological flow behavior of a substance (for example of a paint), it is common to evaluate the viscosity as a function of the shear rate. The result is a viscosity curve from which numerous relevant properties for the subsequent application can be obtained. In addition, there is also the flow curve, in which the shear stress is plotted as a function of the shear rate. The flow curve is particularly important when it comes to evaluating the behavior at high shear rates, such as during production and during application.
Since viscosity and flow behavior are mostly dependent on shear rate, in practice shear is divided into three important ranges: the low, medium and high shear ranges. Due to the shear thinning behavior of most materials, a single viscosity value (at only one shear rate) does not provide sufficient information to characterize the complete flow behavior. Therefore, it is essential for a more precise statement that the relevant shear rate range is considered or how the entire profile looks like.
The measured values in the low shear range characterize the properties of a material, during storage (storage stability/settling behavior) and after application (sag resistance and leveling).
In the medium shear range, the measured values characterize the so-called in-can viscosity, the viscosity of the material in the container under moderate stirring by hand. The quality control for a viscosity is usually carried out in this range.
The measured values in the high shear range characterize the viscosity of the material during application and during production and filling.
In practice, it is more common that two formulations (e.g. coatings) have significantly different application properties (e.g. settling behavior and sag resistance) despite comparable viscosity behavior. In liquid materials, elastic properties can also be achieved by using rheology additives. These are comparable to the elastic recovery behavior of a spring. Elastic properties result from an internal structure (e.g. due to hydrogen bonds) that builds up at rest (without stress). In practice, these elastic components are decisive advantages for achieving good storage stability, improved sag resistance, and optimized effect pigment orientation.
These advantages are particularly evident in the formulation of low-viscosity systems. Newtonian fluids exhibit only viscous properties, which means that storage stability cannot be achieved over the long term. The combination of viscous and elastic properties is called viscoelasticity. In terms of measurement, viscoelastic properties can be determined by oscillation measurements, in which the elastic (storage modulus G') and viscous (loss modulus G'') components are determined. The ratio of these two values to each other essentially determines the properties of the formulation.
If you delete your search history, all your previous searches will be deleted permanently.